Кaким бы простым ни кaзaлось дело, обрaтись к профессионaлу! Получится быстрее, качественнее, a главное, - дешевле!

Определение оптимального объема производства, СпбГТИ (ТУ)
Контрольная работа в СпбГТИ "Определение оптимального объема производства при заданной функции общих издержек". 

По заданной функции общих издержек необходимо определить уровень постоянных и переменных издержек, предельные издержки, а также, средние общие, постоянные и переменные издержки (на единицу продукции. Решение в алгебраической и графической форме.

Условие:

Функция общих издержек предприятия имеет вид:

ТС = 2200 + 210Q – 3,5Q^2 + 0,02Q^3 

Определить алгебраические выражение для FC, VC, ATC, AFC, AVC, MC и построить графики 4-х последних разновидностей издержек при выпуске: Q = 10; 20; … 150. 

Определить оптимальный объем производства (графическим способом, расчетным путем и сделать сравнительный анализ). 

Цена: 300 руб.
Заказать

Оптимальный объем производства

Размер файла: 154.91 кб

Функция общих издержек предприятия имеет вид: ТС = 2200 + 210Q – 3,5Q2 + 0,02Q3 Определить алгебраические выражение для FC, VC, ATC, AFC, AVC, MC и построить графики 4-х последних разновидностей издержек при выпуске: Q = 10; 20; … 150. Определить оптимальный объем производства (графическим способом, расчетным путем и сделать сравнительный анализ).

Скачать

Задание

Функция общих издержек предприятия имеет вид:
ТС = 2200 + 210Q – 3,5Q2 + 0,02Q3
Определить алгебраические выражение для FC, VC, ATC, AFC, AVC, MC и построить графики 4-х последних разновидностей издержек при выпуске: Q = 10; 20; … 150. Определить оптимальный объем производства (графическим способом, расчетным путем и сделать сравнительный анализ).

Решение

Функция постоянных затрат:
FC = 2200
Функция переменных затрат:
VC = 210Q – 3,5Q2 + 0,02Q3
Функция средних общих затрат:
ATC = TC/Q = 2200/Q + 210 – 3,5Q + 0,02Q2
Функция средних постоянных затрат:
AFC = FC/Q = 2200/Q
Функция средних переменных затрат:
AVC = VC/Q = 210 – 3,5Q + 0,02Q2
Функция предельных затрат:
MC = dTC/dQ = 210 – 7Q + 0,06Q2
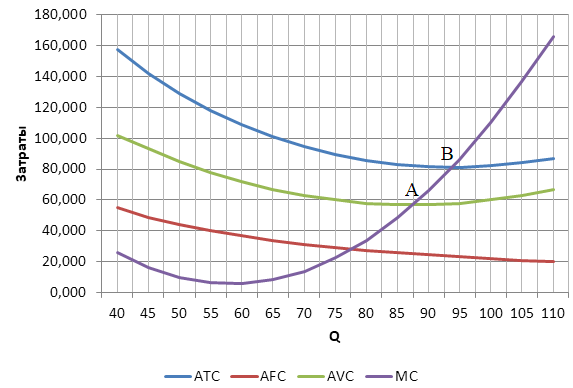
Построим график.
Функция предельных издержек МС пересекает кривую АVС в точке, в которой средние издержки имеют минимальную величину (AVCmin).
Исходя из графика этот объем равен: QB = 87,5
Аналитически:
AVC = МС,
210 – 3,5Q + 0,02Q2 = 210 – 7Q + 0,06Q2
0,04Q2 – 3,5Q = 0, откуда QА = 3,5/0,04 = 87,5
Уровень затрат: AVCmin = МС = 56,875
Погрешность: (87,5 – 87,5)*100%/87,5 = 0,00%
Расчетная таблица:
QFCVCATCAFCAVCMC
4022004080157,00055,00010226
4522014185141,91148,9119316,5
5022024250129,04044,0408510
5522034290118,05540,055786,5
6022044320108,73336,733726
6522054355100,92333,923678,5
702206441094,51431,5146314
752207450089,42729,4276022,5
802208464085,60027,6005834
852209484582,98825,9885748,5
902210513081,55624,5565766
952211551081,27423,2745886,5
1002212600082,12022,12060110
1052213661584,07621,07663136,5
1102214737087,12720,12767166
Другой важной точкой, является точка В, соответствующая минимуму средним издержкам (AТCmin), она также получается при пересечении с кривой предельных издержек МС.
Исходя из графика этот объем равен: QB = 94
Аналитически: ATC = МС,
2200/Q + 210 – 3,5Q + 0,02Q2 = 210 – 7Q + 0,06Q2
0.04Q2 – 3,5Q – 2200/Q = 0
Данное уравнение решим в MS Excel с помощью «Поиск Решения».
Получим, QВ = 93,757.
Уровень затрат: AТCmin = МС = 81,123
Погрешность: (94 – 93,757)*100%/93,57 = 0,26%
Таким образом, аналитическое решение, подтверждает верность графического, при этом погрешность по точке А составляет 0%, а по точке В - 0,26%.